[알고리즘] 동적 계획법 (Dynamic Programming / DP / 다이나믹 프로그래밍)

동적 계획법 (Dynamic Programming)

 

동적 계획법, DP는 복잡한 큰 문제를 여러 개의 작은 문제로 나누어 푸는 방식이다.다이나믹 프로그래밍이라는 이름은 고안자인 Richard Bellman이 붙인 이름인데 Dynamic이라는 단어가 멋져서 그렇게 지어졌으며 실제 원리와는 전혀 상관없다고 한다.반복되어 나오는 작은 문제들을 저장해 두었다가 재활용하기 때문에 직관적으로 '기억하며 풀기' 로 생각하는 것이 좋다.

 

 

왜 사용하는가?

 

피보나치 수를 구하는 재귀함수를 생각해 볼 수 있다.

 

 

 

 

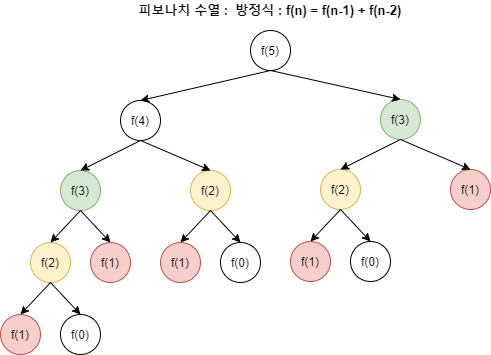
f(n-1)에서 구한 값을 f(n-2)에서 한번 더 구하기 때문에 실행되는 함수의 횟수가 기하급수적으로 증가하게 된다.

그러나 한번 구한 작은 문제의 값을 저장해놓는다면 연산 수가 급격히 감소하여 효율성이 증가한다.  O(n^2) → O(f(n))

 

 

DP 사용 조건

 

두 가지 조건을 만족해야 한다.

1. 겹치는 부분 문제 (Overlapping Subproblems)

: 피보나치 재귀함수를 예로 들었듯이 겹치는 작은 문제가 존재해야 한다.

 

2. 최적 부분 구조 (Optimal Substructure)

: 부분 문제의 최적결과가 전체에도 그대로 적용되어야 한다.

 

 

분할 정복 알고리즘과의 차이

 

분할 정복 알고리즘에 의해 분할된 문제들은 모두 독립적이다.

그러나 DP를 통해 분할되는 작은 문제들은 한번 해결된 문제들을 서로 공유한다는 차이가 있다.

 

분할 정복 알고리즘: 합병 정렬

 

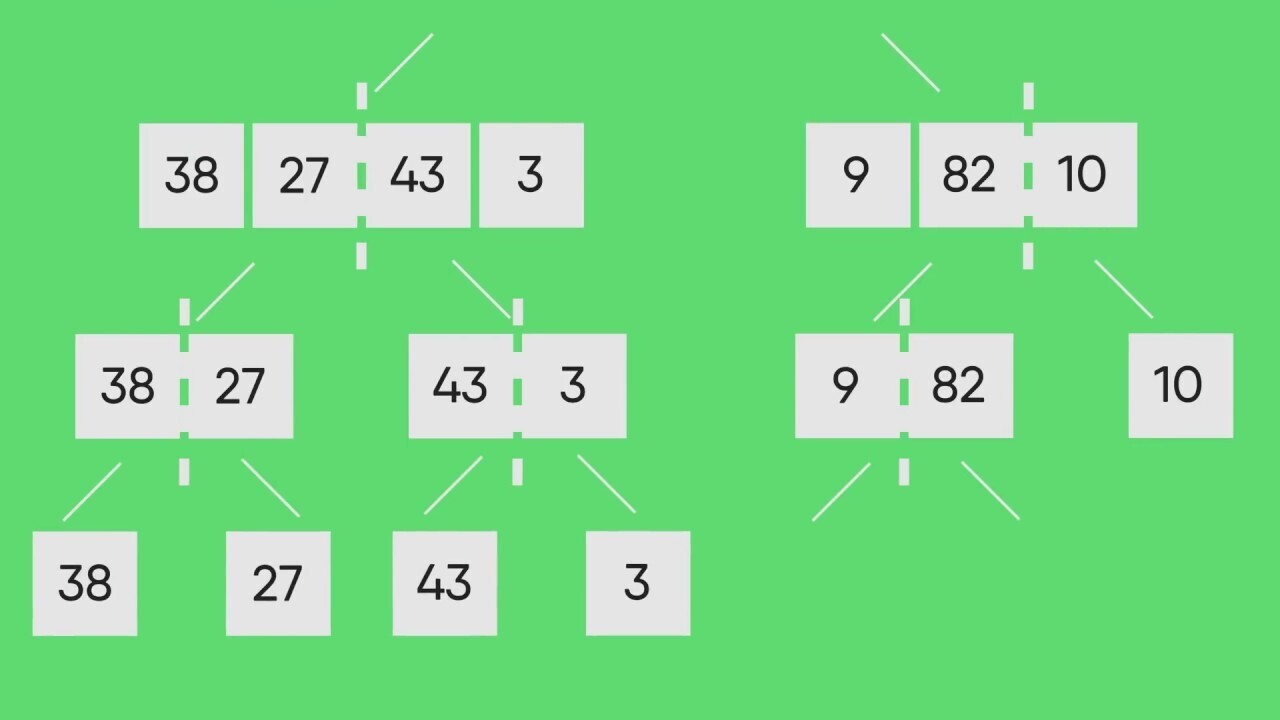
분할 정복의 예인 합병 정렬의 과정 중 하나이다. 위와 같이 분할된 정보는 중복되지 않기 때문에 재사용되지 않는다.

 

 

DP: 피보나치

 

그러나 DP의 피보나치 재귀의 경우 f(2)를 구하기 위해서는 f(1)과 f(0), f(3)를 구하기 위해서는 f(2)와 f(1)이 반복되어 계산되어야 한다. 즉 동일한 문제를 공유한다는 차이가 있다.

 

구현

 

메모이제이션이란?

 

중복된 값을 재사용하기 위한 결과값 리스트나 테이블

캐싱이라고도 한다.

 

Bottom up	Top down
상향식	하향식
반복문으로 구현	재귀함수로 구현
작은 문제로 큰 문제 해결	큰 문제를 해결하기 위해 작은 재귀 함수 호출
메모이제이션 없음	메모이제이션(캐싱) 사용
오버헤드를 줄일 수 있다. 일반적으로 성능이 더 좋다.	오버헤드 가능성이 있다.
점화식 필요

 

Top Down (하향식)

function fibonacciTopDown(n, memo = {}) {
  if (n === 0) return 0;
  if (n === 1) return 1;

  if (memo[n]) {
    return memo[n];
  }

  memo[n] = fibonacciTopDown(n - 1, memo) + fibonacciTopDown(n - 2, memo);

  return memo[n];
}

하향식의 경우 일반적으로 재귀 호출을 하면서 이미 계산한 작은 문제의 결과값을 memo에 저장한다.

그리고 재호출 시 메모이제이션 결과가 있다면 그 값을 사용한다.

 

Bottom Up (상향식)

function fibonacciBottomUp(n) {
  if (n === 0) return 0;
  if (n === 1) return 1;

  const dp = new Array(n + 1);
  dp[0] = 0;
  dp[1] = 1;

  for (let i = 2; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }

  return dp[n];
}

상향식의 경우 가장 작은 0과 1부터 시작하여 반복문 안에서 값들을 dp에 저장하여 활용한다.

 

DP 예제 - 거스름돈 문제

 

 

 

 

위와 같은 단위의 동전의 경우, 그리디 알고리즘으로 거스름돈 최적해를 구할 수 없다.

DP를 사용해서 작은 문제부터 풀 수 있다.

 

다음은 bottom-up 방식을 사용한 javascript 코드이다.

function minimumCoins(n, coins) {
  const dp = new Array(n + 1).fill(Number.MAX_SAFE_INTEGER); // dp 배열 무한대로 초기화
  dp[0] = 0;                                       // 0원 거스르는 동전 개수 -> 0개
  for (let i = 1; i <= n; i++) {                   // 1원부터 650원까지 (작은 문제 -> 큰 문제)
    for (let j = 0; j < coins.length; j++) {       // 500, 300, 50, 10 동전 액면가 배열 순회
      if (coins[j] <= i) {                         // 동전 액면가가 i보다 작거나 같다면
        const sub = dp[i - coins[j]];              // i - 액면가 => sub (부분 문제)
        if (sub !== Number.MAX_SAFE_INTEGER) {     // sub 값이 무한대가 아닌 경우 (조합 존재)
          dp[i] = Math.min(dp[i], sub + 1);        // 해당 값과 sub + 1 작은 값 비교
        }
      }
    }
  }
  return dp[n];
}

const coins = [500, 300, 50, 10];
const n = 650;
console.log(minimumCoins(n, coins));               // 3 출력

 

 

예를 들어 i == 10일 때,

처음으로 coins[j] <= i 가 성립하여 sub = dp[10 - 10] 이 할당된다. 이때 dp[0] = 0이므로 sub는 0이 된다.

dp[10]은 무한대로 처음에 초기화되었기 때문에, sub + 1 = 1과 비교했을 때 최솟값인 1이 dp[10]에 할당된다.

 

i가 거슬러 줘야할 금액인 650이 되면,

dp[640] + 1, dp[600] + 1, dp[350] + 1, dp[150] + 1의 최솟값이 비교된다.

이때, dp[640]과 dp[600], dp[350], dp[150]은 모두 같은 과정을 거쳐 최적해가 도출된 상태이므로 dp[650]의 최적해가 도출된다.

 

 

 

 

 

 

 

 

 

https://chae52.tistory.com/206

DP : Dynamic Programming : 동적 계획법 : 동적 프로그래밍 : 다이나믹 프로그래밍개념 정리/template/상향