[알고리즘] 그리디 알고리즘 (Greedy Algorithm / 탐욕 알고리즘)

그리디 알고리즘 (Greedy Algorithm)

 

그리디 알고리즘은 "현재 상황에서의 최적해를 선택하는 방식"이다.

백트래킹을 통해 추가적인 점검을 하지 않고, 현재 선택지 이외에는 검증을 하지 않는다.

하지만 그 해가 항상 최적해라는 보장을 할 수 없다는 한계가 존재한다.

 

위와 같은 최소 가중치 문제에서, 그리디 알고리즘을 적용하면 7과 10중에 7을 선택하고, 12와 15중에 12를 선택하여 7 + 12 = 19의 가중치를 해로 갖게 된다.

 

그러나 그림을 보면 알 수 있듯이 실제 최소 가중치는 10 -> 5를 선택하는 15이다.

그리디 알고리즘을 적용했을 때, 매 선택마다 부분 최적해는 구했지만, 전체 최적해를 구하지 못한 것이다.

따라서 그리디 알고리즘은 항상 최적해를 보장하지 못한다고 할 수 있다.

 

 

그렇다면 왜 사용할까?

 

이러한 단점들을 모두 극복하는 장점이 있는데, 그것은 바로 '계산 속도'이다.

그리디 알고리즘은 각 단계에서 최적해를 선택하는 것이 아닌, 부분적으로 최적해를 선택하기 때문에 전체적인 계산 비용이 매우 줄어들게 된다.

 

하지만 위의 예시를 보면 실제 최적해와 거리가 매우 먼 문제들에는 적용할 수 없기 때문에, 그리디 알고리즘을 사용하려면 2가지 조건을 만족해야 한다.

 

그리디  알고리즘의 조건

 

1) 탐욕 선택 속성(Greedy Choice Property)

이전의 선택이 이후에 영향을 주지 않아야 한다.

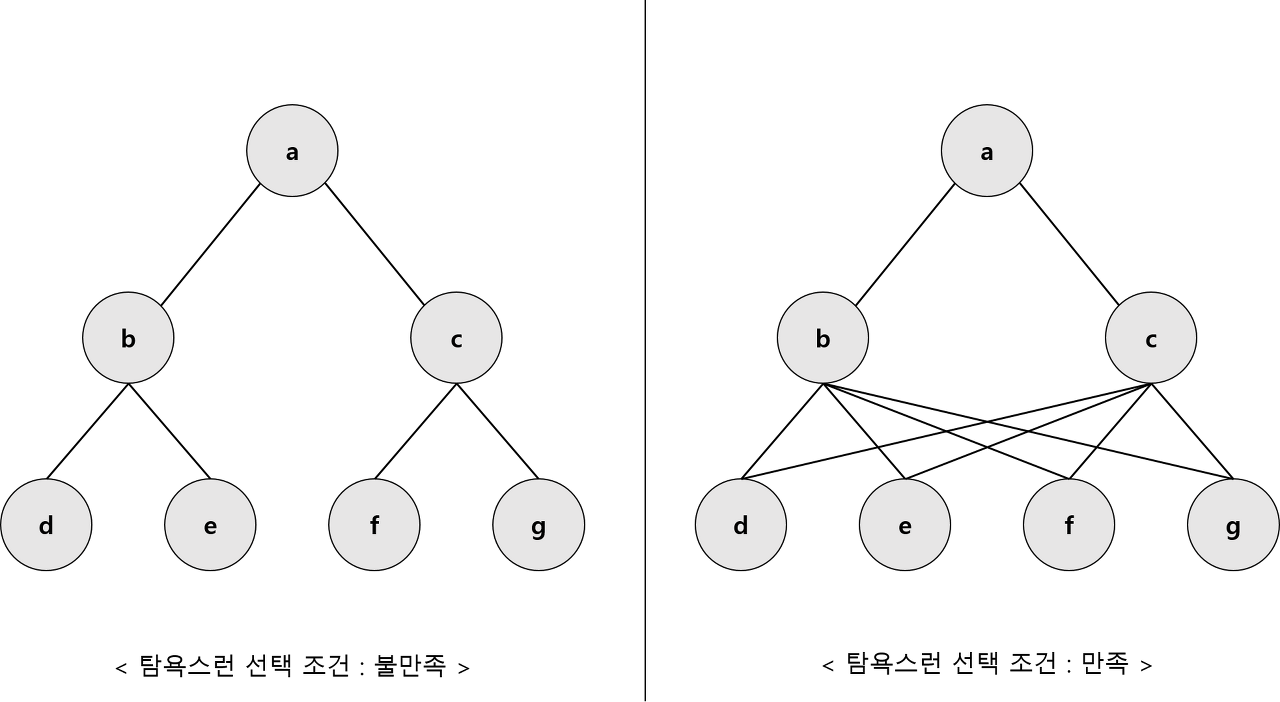
왼쪽의 경우 b,c 선택에 따라 선택지가 다르게 된다. 이런 경우는 선택이 이후 영향을 주므로 그리디 알고리즘을 적용할 수 없다.

오른쪽의 경우 b,c 선택에 관계없이 d,e,f,g의 선택을 할 수 있으므로 탐욕 선택 속성을 만족한다.

2) 최적 부분 구조(Optimal Substructure)

부분 문제의 최적결과가 전체에도 그대로 적용되어야 한다.

최대 정점의 합을 구하는 문제일 때, 부분 문제에서 30을 선택한 결과가 전체에도 그대로 적용된다.

 

그리디  알고리즘 예제 - 부분 배낭 문제

 

부분 배낭 문제는 정해진 용량의 배낭에 가장 많은 가치를 가진 물건들을 채우는 문제이다.

물건을 쪼개서 담을 수 있다는 특징이 있는 문제이다.

 

 

그리디 알고리즘에 따라, 가장 높은 가치의 물건들로 배낭을 채우기 위해 무게당 가치가 높은 순으로 배낭에 채운다.

초록 2L -> 파랑 3L -> 보라 2L 를 담고, 빨강 1L는 쪼개 담아 최적해를 구할 수 있다.

물건을 쪼개 넣는 것이 가능하기 때문에, 무게당 가치 순으로 선택하는 것이 이후에 영향을 주지 않고 최적해를 찾을 수 있다. 따라서 탐욕 선택 속성을 만족한다.

또한, 단계에서 선택한 물건을 배낭에 넣었을 때 남은 여유 공간은 다른 물건들을 선택하는 문제로 축소되므로 최적 부분 구조를 만족한다.

 

 

그리디  알고리즘 예시 - 거스름돈 문제

 

 

위와 같은 종류의 동전들이 있다.

줘야 할 거스름돈이 870원이라면, 그리디 알고리즘에 따라 다음과 같이 최소의 동전을 구할 수 있다.

 

500원 1개, 100원 3개, 50원 1개, 10원 3개

 

동전의 작은 단위와 큰 단위가 모두 배수 관계를 이루기 때문에,

큰 단위의 선택은 무조건 작은 단위를 여러 개 선택하는 것과 같게 된다. (500원 = 100원*5 = 50원*10 = 10원*50)

따라서 큰 단위부터 선택하면 항상 최적해를 얻을 수 있다.

배수 관계에 따라 각 단계 선택이 다음 선택에 영향을 주지 않으며, 각 단계에서 동전을 고른 후 남은 거스름돈으로 다시 동전을 선택하는 부분 문제로 축소되므로 탐욕 선택 속성과 최적 부분 구조를 모두 만족한다.

 

배수 관계가 아닌 경우에는?

 

배수 관계가 아닌 거스름돈 문제의 경우에도 그리디 알고리즘을 적용할 수 있을까?

위와 같은 동전 단위가 있다.

650원을 거슬러 주어야 할 때, 그리디 알고리즘을 적용하면 다음과 같다.

500원 1개, 50원 3개

 

그러나 실제 최적해는 다음과 같다.

300원 2개, 50원 1개

이전과 다른 점은 무엇일까?

300원은 500원의 약수가 아니다. 따라서 500원은 300원을 대체하여 더 적은 숫자로 반환할 수 있다는 최적해를 보장할 수 없다.

 

이처럼 그리디 알고리즘으로 최적해를 얻을 수 없는 문제들이 존재한다.

따라서 그리디 알고리즘의 조건을 충분히 만족하는지 검증하는 과정은 중요하며, 풀이가 불가능할 경우에는 동적 계획법(Dynamic Programming) 등의 다른 알고리즘을 사용해야 한다.

 

[알고리즘] 동적 계획법 (Dynamic Programming / 다이나믹 프로그래밍)